noise_predictionモデルとv_predictionモデルの損失

　Stable-Diffusionのv1系は画像に加わったノイズを予測するモデルですが、v2の一部はvelocityというものを予測しています。この2つは損失関数が違うのでlossで比べられません。経験的にv_predictionモデルの方が3倍くらいlossが大きくなるイメージですが、数学的に確認していきます。
　

ノイズが加わった画像について

元の画像を $x_0$ 、ノイズを $\epsilon$ とすると時刻 $t\in [1,\cdots,1000]$ でノイズが加えられた画像は $x_t=\sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}}\epsilon$ という式で表されます。 $x_0$ はVAEエンコーダの出力である潜在変数なので、平均0で分散1の正規分布に従っています。ノイズはそもそも実装として平均0で分散1の正規分布です。めんどくさいので $a_t=\bar{\alpha_t},\ \sigma_t=\sqrt{1-\bar{\alpha_t}}$ とします。すると画像の分散は $a_t^2$ 、ノイズの分散は $\sigma_t^2$ になります。

velocity[1]について

　 $a_t^2+\sigma_t^2=1$ であることに注目すると、時刻 $t$ ごとにある角度 $\phi_t$ があって、 $a_t=\cos \phi_t,\ \sigma_t=\sin \phi_t$ で表されます。そうすると $x_t=\cos \phi_t x_0 + \sin \phi_t \epsilon$ となります。これを角度で微分したものがvelocityです。 $v=\frac{dx_t}{d\phi_t}= - \sin \phi_t x_0 + \cos \phi_t \epsilon= a_t \epsilon - \sigma_t x_0$ となります。図にすると以下のようになります。

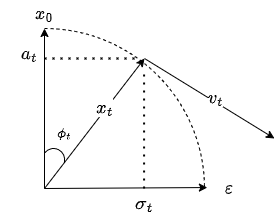
ノイズを加えていく拡散過程を円運動ととらえて、velocityはその速度になるわけですね。

信号対雑音比

　ここで信号対雑音比(s/n比、SNR)というものを紹介します。これは $\mathrm{SNR}=\frac{\text{信号の分散}}{\text{雑音の分散}}=\frac{a_t^2}{\sigma_t^2}$ で求まり、ノイズが小さい画像は大きくなり、ノイズが大きい画像ほど小さくなります。この信号対雑音比を考えると、ノイズ $\epsilon$ を予測するモデルとvelocity $v$ を予測するモデルと元の画像 $x_0$ を予測するモデルが統一的に考えられます。モデルが予測した値に $\hat{}$ をつけるとそれぞれのモデルの損失の関係は以下のようになります。[2]で紹介されています。
$\begin{eqnarray} \|\epsilon - \hat{\epsilon}\|^2 &=& \|\frac{x_t-a_t x_0 }{\sigma_t} - \frac{x_t-a_t\hat{x_0}}{\sigma_t}\|^2 \\ &=& \|-\frac{a_t}{\sigma_t}(x_0 - \hat{x_0})\|^2 \\ &=& \frac{a_t^2}{\sigma_t^2}\|x_0 - \hat{x_0}\|^2 \\ &=& \mathrm{SNR}(t)\|x_0 - \hat{x_0}\|^2 \end{eqnarray}$

入力におけるノイズが占める割合が少ないとき(SNRが大きいとき)は $x_0$ の予測は簡単で、 $\epsilon$ の予測が難しくなります。この事実が損失関数の関係に現れていますね。極端な話をするとSNRが0のとき、つまり入力がノイズのときノイズ予測モデルでは損失が0になります。入力をそのまま出力するだけなんだから当然ですね。

$\begin{eqnarray} \|v - \hat{v}\|^2 &=& \|a_t \epsilon-\sigma_t x_0 - (a_t \hat{\epsilon} - \sigma_t\hat{x_0})\|^2 \\ &=& \|a_t(\epsilon - \hat{\epsilon}) -\sigma_t(x_0 - \hat{x_0})\|^2 \\ &=& \|a_t(\frac{x_t-a_t x_0 }{\sigma_t} - \frac{x_t-a_t\hat{x_0}}{\sigma_t}) -\sigma_t(x_0 - \hat{x_0})\|^2 \\ &=& \|-\frac{a_t^2}{\sigma_t}(x_0-\hat{x_0}) -\sigma_t(x_0 - \hat{x_0})\|^2 \\ &=& |-\frac{a_t^2+\sigma_t^2}{\sigma_t}(x_0 - \hat{x_0})\|^2 \\ &=& |-\frac{1}{\sigma_t}(x_0 - \hat{x_0})\|^2 \\ &=& (\frac{1}{\sigma_t^2})\|(x_0 - \hat{x_0})\|^2 \\ &=& (\frac{a_t^2+\sigma_t^2}{\sigma_t^2})\|(x_0 - \hat{x_0})\|^2 \\ &=& (\mathrm{SNR}(t)+1)\|x_0 - \hat{x_0}\|^2 \\ &=& \frac{\mathrm{SNR}(t)+1}{\mathrm{SNR}(t)}\|\epsilon - \hat{\epsilon}\|^2 \end{eqnarray}$

つまりv_predictionモデルは $\frac{\mathrm{SNR}(t)+1}{\mathrm{SNR}(t)}$ だけ損失が大きくなるということですね。これがどのくらいの値なのか調べてみましょう。

import torch
from diffusers import DDPMScheduler
import matplotlib.pyplot as plt
scheduler = DDPMScheduler.from_pretrained("stabilityai/stable-diffusion-2", subfolder="scheduler")

timesteps = torch.arange(0,1000)

def get_snr(
    scheduler, 
    timesteps: torch.IntTensor,
) -> torch.FloatTensor:

    sqrt_alpha_prod = scheduler.alphas_cumprod[timesteps] ** 0.5
    sqrt_alpha_prod = sqrt_alpha_prod.flatten()

    sqrt_one_minus_alpha_prod = (1 - scheduler.alphas_cumprod[timesteps]) ** 0.5
    sqrt_one_minus_alpha_prod = sqrt_one_minus_alpha_prod.flatten()

    return (sqrt_alpha_prod / sqrt_one_minus_alpha_prod) ** 2

snr = get_snr(scheduler, timesteps)

plt.xlabel("timesteps")
plt.ylabel("(snr+1)/snr")
plt.plot(timesteps,(snr+1)/snr)

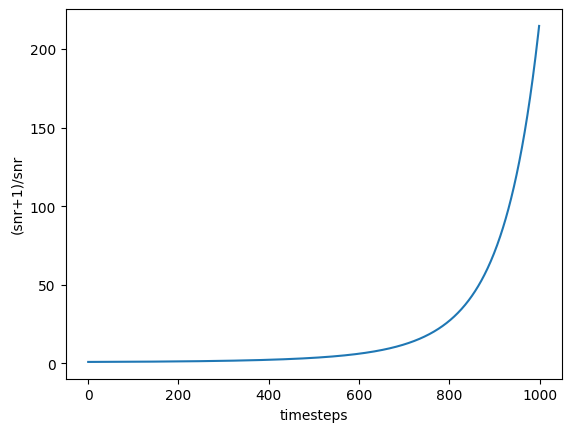
こうしてみると $t$ が大きいとき、つまりノイズが大きいときに損失が大きくなりやすいですね。グラフ見ただけではわかりませんが、時刻が0に近いとき値は1に近づいています（式を考えれば当然ですけど）。velocityを予測するモデルでは、 $\epsilon$ と $x_0$ の両方を予測する必要があるため、ノイズ予測モデルのようにノイズが大きいときは予測が簡単という関係になりにくいです。よって各時刻における予測難易度のバランスがとれているということですね。このグラフの平均をとればv_predictionでどのくらいlossが大きくなるはずか計算できるのかなと思ったんですが、そうじゃないみたいですね。単純に平均すればいいってわけじゃないみたいですね。

v_predictionモデルでnoise_predictionのように学習する？

v2系はv1系に比べて評価が低いです。理由として考えられるのは以下の三点です。

テキストエンコーダが悪い
あんな画像を学習しないのが悪い
v_predictionモデルが悪い

1.に関してはよく知りませんが、v1系と違うものなので可能性はあります。

2.に関してはv2系はあんな画像を結構弾いたらしいので、基盤モデルとしてアニメ調の画像の性能が悪いのかもしれません。

そして3.が今回の話です。ノイズ予測モデルと比べて、ノイズが大きいときの損失が大きくなるので、大まかな要素の学習を優先して、細部の学習を怠ってしまうのかもしれません。これが原因ならば幸いファインチューニングで修正できる可能性はあります。損失に $\frac{\mathrm{SNR}(t)}{\mathrm{SNR}(t)+1}$ をかけるだけでノイズ予測モデルと同様の学習ができます。