2023-06-28

Adafactorについて

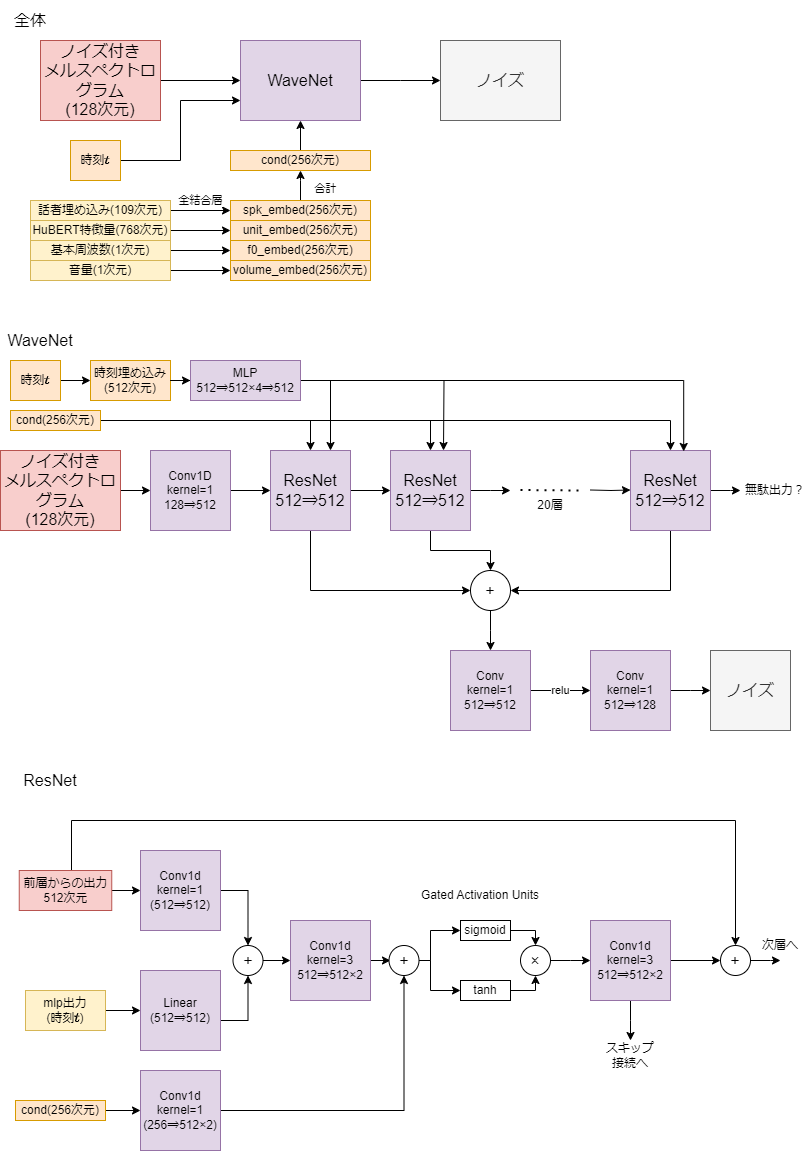
　今回はなぞのおぷてぃまいざーであるAdafactorについて論文の内容を見ていきます。
arxiv.org

概要

　AdafactorはAdamを元にした最適化アルゴリズムで、メモリ容量の削減とパラメータスケールに応じた学習率の調整を行う手法です。勾配の二乗指数平均をランク1行列で近似することによって、サイズを減らしています。勾配の指数平均の方はカットして、その代わりに色んな工夫がなされています。

最適化アルゴリズム(Optimizer)について

　以下の神記事に任せます。
qiita.com

Adamについて

　ステップ数を $t$ と、 $\beta_1, \beta_2$ が1よりちょっと小さい値を設定するハイパーパラメーターで、学習率が $\alpha_t$ 、更新対象のニューラルネットワークを $f$ で重みを $w$ とします。するとAdamの更新ステップは以下の通りです。
$1.\ g_t = \nabla_w f \\ 2.\ m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t \\ 3.\ v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\ 4.\ \hat{m_t} = m_t / (1-{\beta_1}^t) \\ 5.\ \hat{v_t} = v_t / (1-{\beta_2}^t) \\ 6.\ w_t = w_{t-1} - \alpha_t \hat{m_t}/(\sqrt{\hat{v_t}}+\epsilon)$
　 $\epsilon$ は分母が $0$ になるのを防ぐための微小量です。2行目が勾配の指数平均であり、ここでは一次モーメントと呼ぶことにします。3行目が勾配の二乗指数平均であり二次モーメントと呼びます。一次モーメントは過去の移動経路を元に慣性をつけるような役割となり、うろうろ動くことを防止します。二次モーメントは過去の移動の大きさを元に移動を制限するような項目であり、変化量が大きすぎるパラメータにじっとしておけ！と命令することでこれもまたうろうろ動くことを防止できます。4行目、5行目に関してはバイアス補正と呼ばれるもので、後で紹介しますが、学習の初期ステップでの精度低下を補正するものになります。 $t$ が大きいときは係数が1に近づき効果がないことが分かると思います。
　このAdamという最適化関数はもはやディープラーニング業界のデファクトとなっています。ただし明確な欠点として、各パラメータの一次モーメントと二次モーメントを記憶しなければならないということがあります。学習対象のパラメータサイズの二倍のメモリが追加で必要になるので、大きなモデルを学習するのが難しくなります。対策として記憶精度を8bitにするbitsandbytesや、CPUにオフロードするdeepspeed等がありますが、Adafactorは、二次モーメントのサイズを小さくする手法になります。

二次モーメントの低ランク近似

　重み行列 $W^{(n,m)}$ に対して、二次モーメント $V^{(n,m)}$ があるとします。低ランク近似 $V^{(n,m)} \fallingdotseq R^{(n,k)}S^{(k,m)}$ によってメモリ効率を上げることを考えます。一般的に低ランク近似には特異値分解が用いられます。特異値分解はフロベニウスノルムによる距離を基準にした低ランク近似になります。以前の記事を参照してください。しかし各ステップごとに二次モーメントを特異値分解をするのは、計算量が大きくなり非効率的です。さらに二次モーメントは平方根をとることから非負である必要がありますが、特異値分解による低ランク近似は非負性を保証しません。
　そこで論文では一般化KLダイバージェンス $d(p,q)=p\log\frac{p}{q}-p+q$ というものを距離とした近似を行います。この距離は $\log$ の中身をみれば分かる通り、 $p,q$ が両方0より大きい（または小さい）とき定義できますが、二次モーメントは二乗指数平均なので全要素が正になります(0になる可能性はある)。 $x\log x \geq x - 1$ という不等式から、 $x=\frac{p}{q}$ を代入すると、 $d(p,q)\geq 0$ で等号成立条件は $p=q$ になることがわかります。 $d(p,q)=d(q,p)$ が成り立つとは限らないので正確には距離ではないですが、まあそれはおいときます。この距離を基準にした低ランク近似の最適解は、一般のランク $k$ に対しては簡単には求められないらしいですが、ランク $1$ のときは簡単に求められます。ランク $1$ というのは $R$ が列ベクトル、 $S$ が行ベクトルになるという意味です。このとき $RS$ の $(i,j)$ 要素は $R$ の $i$ 番目の要素 $R_i$ と $S$ の $j$ 番目の要素 $S_j$ の積になります。つまり $(RS)_{ij}=R_iS_j$ になります。このとき $V$ と $RS$ の距離は、
$\begin{eqnarray} & & \displaystyle{\sum_{i,j}^{n,m}d(V_{ij},(RS)_{ij})} \\ &=& \displaystyle{\sum_{i,j}^{n,m}V_{ij}\log\frac{V_{ij}}{R_iS_j}-V_{ij}+R_iS_j} \\ &=& \displaystyle{\sum_{i,j}^{n,m}V_{ij}\log V_{ij}} - \displaystyle{\sum_{i,j}^{n,m}V_{ij}\log R_{i}} - \displaystyle{\sum_{i,j}^{n,m}V_{ij}\log S_j} - \displaystyle{\sum_{i,j}^{n,m}V_{ij}} + \displaystyle{\sum_{i,j}^{n,m}R_iS_j} \end{eqnarray}$
となり、距離が下に凸( $\frac{\partial^2}{\partial q^2}d(p,q)=\frac{p}{q^2} \geq 0$ )であることから、最適解は $R_i,S_j$ で微分して0になる値になります。
$\displaystyle{-\sum_{j=1}^{m}\frac{V_{ij}}{R_i}} + \displaystyle{\sum_{j=1}^{m}S_j} = 0 \ \Rightarrow \ R_i = \frac{\sum_{j=1}^{m}V_{ij}}{\sum_{j=1}^{m}S_j} \\ \displaystyle{-\sum_{i=1}^{n}\frac{V_{ij}}{S_j}} + \displaystyle{\sum_{i=1}^{n}R_i} = 0 \ \Rightarrow \ S_j = \frac{\sum_{i=1}^{n}V_{ij}}{\sum_{i=1}^{n}R_i}$

このままでは $R$ を計算するために $S$ が必要で、 $S$ を計算するために $R$ が必要で・・・と無限ループに陥ります。そこで最適解について、 $RS = (\alpha R)(S/\alpha)$ であることから、どっちかになんかをかけてどっちかにその逆数をかけたものも同じく最適解になります。この性質をつかえば、 $\displaystyle{\sum_{j=1}^{m}S_j}=1$ になるよう正規化してあるような最適解を作ることができます。このとき、
$R_i = \displaystyle{\sum_{j=1}^{m}V_{ij}} \\ S_j = \frac{\sum_{i=1}^{n}V_{ij}}{\sum_{i=1}^{n}R_i} = \frac{\sum_{i=1}^{n}V_{ij}}{\sum_{i=1}^{n}\sum_{j=1}^{m}V_{ij}}$
となります。 $R$ は $V$ の行ごとの和であり、 $S$ は $V$ の列ごとの和を正規化したものになります。これによって計算可能になります。さらに、指数平均と行や列ごとの和の順序が可換であることから、 $R,S$ の指数平均を計算するだけで済みます。

つまり、
$V_t = \beta_2 V_{t-1} + (1-\beta_2){G_t}^2$ となりますが、
$R_{t,i} = \displaystyle{\sum_{j=1}^{m}} (\beta_2V_{t-1,ij} + (1-\beta_2){G_{t,ij}}^2) = \beta_2 R_{t-1,i} + (1-\beta_2)\displaystyle{\sum_{j=1}^{m}}{G_{t,ij}}^2$
であり、わざわざ次ステップの $V_t$ を計算せず $R_{t-1}$ から直接 $R_t$ が求められます。 $S_t$ に関しても、分子は列ごとの和ですから同様に計算できて、分母は正規化定数に過ぎないので分子を計算してから求めればよいです。

　この原理を使ったアルゴリズムは以下の通りになります。
$1.\ G_t = \nabla_W f \\ 2.\ R_t = \beta_2 R_{t-1} + (1-\beta_2)\displaystyle{\sum_{j=1}^{m}}{G_{t,*j}}^2 \\ 3.\ C_t = \beta_2 C_{t-1} + (1-\beta_2)\displaystyle{\sum_{i=1}^{n}}{G_{t,i*}}^2 \\ 4.\ \hat{V_t} = (R_tC_t/\displaystyle{\sum_{i=1}^n}R_t)/(1-{\beta_2}^t) \\ 5.\ W_t = W_{t-1} - \alpha_t G_t / (\sqrt{\hat{V_t}}+\epsilon)$
Adamと違って大文字になっているのは行列になっているからです。なんで $S$ が $C$ になってるの？とかなんで $R$ 側を正規化することにしたの？とか思いますが論文にそう記述されているからしょうがないです。一次モーメントは正負がばらばらで一般化KLダイバージェンスが定義できないので、同様の操作はできませんが、Adamのアルゴリズムをそのまま適用することも可能です。ただし論文では二次モーメントのみで何とかなるような工夫が色々議論されています。

二次モーメントの問題

二次モーメントのハイパーパラメータである $\beta_2$ は、指数平均でどれだけ過去の情報を大事にするかという数値です。このパラメータは大きくしても小さくしても問題がでてくるようです。大きくすると、過去の情報を大事にするわけですが、学習初期に $V_t$ の収束が遅くなり、安定しなくなります。そのため学習初期の学習率を小さくするwarm upが必要となります。逆に小さくすれば、 $V_t$ が早期に収束し、初期段階の不安定性がなくなりますが、 $V_t$ が振動しやすくなって、モデル自体の収束に悪影響を及ぼします。

Update Clipping

前節の問題を解決するため、勾配クリッピングのような手法が提案されています。Update Clippingでは最終的な更新行列である $U_t=G_t/\sqrt{\hat{V_t}}$ に対して、以下の指標を使います。
$\mathrm{RMS}(U_t) = \sqrt{\mathrm{Mean}({G_t}^2/\hat{V_t})}$
ようするに現在の二乗勾配とその指数平均との比をとって要素ごとに平均しています。平均との比なので、1から大きく離れていると不安定性の原因となり得ます。そこで、閾値 $d$ に対して、 $\hat{U_t}=U_t/\mathrm{max}(1,\frac{\mathrm{RMS}(U_t)}{d})$ として $\mathrm{RMS}(\hat{U_t})\leq d$ になるようクリッピングします。

$\beta_2$ のスケジューリング

　もう一つの解決法として、学習初期段階では $\beta_2$ を小さくして、だんだん大きくしていくという解決策があります。実はAdamの4,5行目の謎のスケーリングはこの戦略を実現しています。 $\beta_t = \beta\frac{1-\beta^{t-1}}{1-\beta^t}$ という風にスケジューリングすることを考えます。 $0 < \beta < 1$ のとき、 $\beta_1=0, \beta_{\infty} = \beta$ となり $0$ から $\beta$ に増加していきます。ここで、
$\begin{eqnarray} \hat{v_t} &=& \frac{v_t}{1-\beta^t} \\ &=& \frac{\beta\hat{v_{t-1}} + (1-\beta){g_t}^2}{1-\beta^t} \\ &=& \frac{\beta}{1-\beta^t}\hat{v_{t-1}} + \frac{1-\beta}{1-\beta^t}{g_t}^2 \\ &=& \beta\frac{1-\beta^{t-1}}{1-\beta^t}v_{t-1} + \frac{(1-\beta^t) - (\beta - \beta^t)}{1-\beta^t}{g_t}^2 \\ &=& \beta\frac{1-\beta^{t-1}}{1-\beta^t}v_{t-1} + (1- \beta\frac{1-\beta^{t-1}}{1-\beta^t}){g_t}^2 \\ &=& \beta_t v_{t-1} + (1-\beta_t){g_t}^2 \end{eqnarray}$
となって、スケーリングとスケジューリングが同値になることが分かります。しかし論文ではこれを使うのではなく、 $\beta_t = 1-\frac{1}{t^c}$ というスケジューリングを行うそうです。この理由も長々と数式が書かれていましたが、面白くなさそうなのでカット。

Relative Step Size

　学習率を絶対的に定義するのではなく、パラメータスケールに基づいて相対的に定義します。
$\alpha_t = \mathrm{max}(\epsilon_2,\mathrm{RMS}(W_{t-1}))\rho_t$
ここで $\rho_t$ はスケジューリングのための係数です。また重みが0で初期化されているときでも対応できるように、 $\epsilon_2$ で下限をとっておきます。今まで結構理論立てて説明していた割に、この部分はさらっとした説明と実験結果のみで終わっています。

最終的なアルゴリズム

$1.\ \alpha_t = \mathrm{max}(\epsilon_2,\mathrm{RMS}(W_{t-1}))\rho_t \\ 2.\ G_t = \nabla_W f \\ 3.\ R_t = {\beta_2}_t R_{t-1} + (1-{\beta_2}_t)\displaystyle{\sum_{j=1}^{m}}({G_{t,*j}}^2+\epsilon _1) \\ 4.\ C_t = {\beta_2}_t C_{t-1} + (1-{\beta_2}_t)\displaystyle{\sum_{i=1}^{n}}({G_{t,i*}}^2+\epsilon _1) \\ 5.\ V_t = R_tC_t/\displaystyle{\sum_{i=1}^n}R_t \\ 6.\ U_t=G_t/\sqrt{V_t} \\ 7.\ \hat{U_t}=U_t/\mathrm{max}(1,\frac{\mathrm{RMS}(U_t)}{d}) \\ 8.\ W_t = W_{t-1} - \alpha_t \hat{U_t}$

　特に説明が見つからなかったですが、 $\epsilon_1$ は二乗勾配が0にならないようにする微小量です。これは一般化KLダイバージェンスが0で定義できないことからきていると思います。これによって6行目の分母に足す微小量は必要なくなります。論文ではハイパーパラメータを以下のように設定しています。
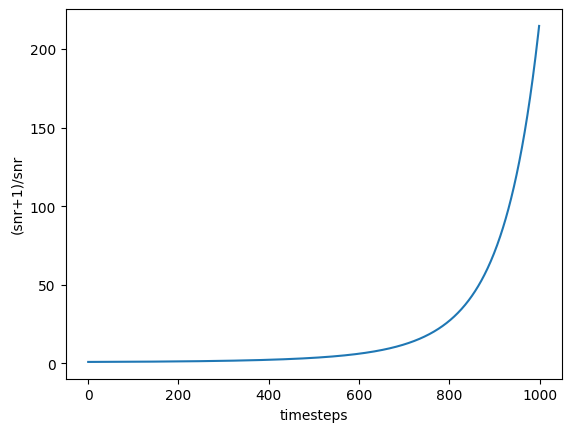
$1.\ \epsilon_1 = 10^{-30} \\ 2.\ \epsilon_2 = 10^{-3} \\ 3.\ d=1 \\ 4.\ \rho_t = \mathrm{min}(10^{-2},\frac{1}{\sqrt{t}})\ \ or\ \ \mathrm{min}(10^{-6}\times t,\frac{1}{\sqrt{t}}) \\ 5.\ {\beta_2}_t = 1 - t^{-0.8}$

$\rho_t$ について、1個目はwarm upなし、2個目はwarm upありになります。実際に見てみましょう。

10000ステップまで固定で、その後は無理関数的に減少していきます。warm upの場合は10000ステップまで線形に増加して、warm upなしの場合と合流します。
ちなみにバイアス項等の重みが行列ではなくベクトルの場合は低ランク近似を行わないこと以外は同じです。

実装

transformersによって実装されています。

( lr = None, eps = (1e-30, 0.001), clip_threshold = 1.0, decay_rate = -0.8, beta1 = None, weight_decay = 0.0, scale_parameter = True, relative_step = True, warmup_init = False )

デフォルトの設定は論文通りになっているようですね。一次モーメントも利用するbeta1や、重み減衰を実装するweight_decayなども設定できるようですね。scale_parameterが $\mathrm{RMS}(W_{t-1})$ によるスケーリング、relative_stepは学習率を無視して $\rho_t$ を使うという項目になります。

Stable diffusionの学習における考察

　Stable-diffusionの、特にLoRA学習でよく使われているみたいです。学習率を自動で決めてくれる代わりに、収束が遅いといった印象のようですね。実際LoRAの学習で使う場合に注意しなければいけない点が結構あると思います。
1. 学習率が自動で決まるという触れ込みだが、学習率に関わるハイパーパラメータは存在する。
学習率は $\epsilon_2$ や $\rho_t$ といったハイパーパラメータに影響します。といってもなぜか $\rho_t$ はハードコーディングされていて設定できないんですけどね(relative_stepで無効にすることはできる)。たとえばLoRAのUP層は初期値が0なので、学習初期はデフォルトの設定だと1e-5に固定されます。これは小さすぎる気がしますね。収束が遅いと呼ばれる原因がこれなら、ここを変えてみるのもありかもしれません。
2. 一次モーメントを使わないので収束が遅い？
Adafactorの収束が遅いのは、一次モーメントを使っていないことも原因かなと思います。メモリに余裕があるならbeta1を設定してみるのもいいかもしれません。
3. rank(dim)の低いLoRAに対してメモリ効率化効果が薄い
Adafactorは二次モーメントの低ランク近似を行いますが、そもそもLoRAは重みそのものに低ランク近似を行っているので、rankの低いLoRAを学習する場合、メモリ容量の削減効果は薄くなります。
4. ステップ数が少ないと学習率スケジューリングの効果がない、warmupの設定は危険
relative_stepをTrueにしたとき、Adafactorの学習率スケジューリングは上のグラフにある通り10000ステップまで定数になります。LoRA学習時はそんなに学習することあまりないと思うので、ほとんどの場合定数スケジューラーになります。さらにwarm upにいたっては、10000ステップまで線形に上昇していくので、むしろ良くないと思います。しかもこの10000ステップという基準は設定で変えられません・・・。
5. DyLoRAとの相性が悪い
DyLoRAは1ステップごとにLoRAの各列各行を選んで更新するので、Adafactorと併用できないようですね。

2023-06-26

DDSP-SVCについて

　こんかいはー、DDSP-SVCがどんな感じか見てみたのでメモしておきます。RVCに対するメリットデメリットなども考察していきます。
実装は以下を参考にしました。
github.com

全体像

　DDSP-SVCは拡散モデルベースの音声変換モデルです。HuBERT特徴量・基本周波数（ピッチ）・音量・話者IDを条件としてメルスペクトログラムを生成します。音声波形の生成には学習済みのHiFi-GANなるものを使っているようです。音声変換時は画像生成(Stable diffusionとか)のときにimg2imgと呼ばれているような構造を使います。

　訓練時は時刻 $t=1,\cdots, k_{\mathrm{max}} \leq 1000$ までステップごとにランダムに選び、時刻に応じてノイズを加えてそれを予測するように学習します。音声変換時は時刻 $k$ を選んで、 $1,\cdots,k$ のノイズ除去ループを実行して最終的に時刻 $t=0$ の状態を得ます。ただしループは1個ずつではなく、何個かスキップしながら実行します。図中のノイズ除去ループ部分はイメージがつきやすいDDPMによる実装になってますが、実際にはサンプラーによって違います。

モデル構造

　WaveNetを元にした構造のモデルになります。

　ResNetが20層のWaveNetになっています。ただしWaveNetと違って膨張畳み込みは使わず（dilation=1）、因果的な畳み込み（過去の情報のみを使う畳み込み）でもないです。VITSもそうでしたが、単なる畳み込みで十分なのかな？あと時刻埋め込みと条件埋め込みでは入力される場所が少し違いますが、この辺の違いは何を意味しているんでしょうかね？

訓練

　訓練対象のモデルは、WaveNetと各条件を埋め込む全結合層のみとなります。HiFi-GANは学習しません。色々なモジュールを学習するRVCと違ってかなりわかりやすいですね。しかもRVCは推論時に使わないモジュールを学習する必要があったりと面倒です。ただしRVCは音声波形を生成するGAN部分まで学習しますが、DDSP-SVCはメルスペクトログラムを生成する部分までしか学習しません。その辺がどのくらい影響を与えるんでしょうかね。まあDDSP-SVCだってGANを学習してもいいんでしょうが。
　時刻いくつまでを学習するかを設定する項目(k_step_max)があるみたいです。DDSP-SVCではノイズ除去は途中からしか行わないので、全ステップ学習する必要性はなさそうですね。

推論

　全体像で書いた通り、変換したい音声のメルスペクトログラムに一定のノイズを加え、そこからノイズ除去することによって音声を変換します。画像生成モデルと同様に、推論時は時刻をある程度スキップします。
設定項目としてk_stepとspeedupがあります。名前は上のリンクにあるPipelineにしたがっています。k_stepは初期時刻をいくつにするかという項目で、Stable diffusion的にいうと、 $\frac{k_{\mathrm{step}}}{1000}$ がDenoising strengthになります。speedupは時刻をどれだけスキップするかの項目で、 $\frac{1000}{speedup}$ がsampling stepになります。またサンプラーは画像生成モデルでも見たことがあるやつが設定できますね。

DDSP-SVCのすごいと思われるところ

　DDSP-SVCがすごいと思うのは、以下の2点です。
1. 精度と速度のトレードオフを調整できる
　推論時に時刻をどのくらいスキップするかを設定することで、精度と速度を調節できます。音声変換の場合はリアルタイムで行いたいときは速度重視、そうでないときは精度重視、などと設定することができます。またGPU性能に応じて変更することもできますね。
2. 元の音声に対する忠実度と変換先の音声に対する精度を調整できる
　入力した音声にどのくらいノイズを与えるかで、変換の強さを調整することもできます。これもかなり使えそうですよね。
　RVCでも前者は検索対象の特徴量を制限したり、後者は線形補間の係数を調整することで同じようなことができそうではありますが、DDSP-SVCほど正確には調整できなそうな気がします（多分）。

DDSP-SVCで気になるところ

1. Classifier Free Guidanceを使ってない
　DDSP-SVCではCFGを使っていません。画像生成モデルでもノイズの少ない状況ではCFGはあまり意味がないということが分かっているので、img2img(というかaudio2audio?)しかしないDDSP-SVCには必要ないのかもしれません。適用したら精度が良くなるのか気になりますが、計算量が2倍になるので結局実用性もなさそうです。というかそもそも無条件の埋め込みって何を入力したらいいんだ？
2. LoRAを使えるのか
　LoRAは画像生成モデルと同様に実装できますが、どのくらいの精度でできるのか気になりますね。ただLoRAを適用するほどモデルが大きくなさそうなのと、話者IDによって複数話者対応のモデルを作れることから、そこまで意味がないのかも？
3. 最後のResNetブロックの出力が無駄になっている
　ResNetブロックは次層への入力と最終出力へのスキップ接続の二つを出力しますが、最後のResNetブロックには次層なんてありません。それにもかかわらず次層への入力も出力する形になっているようです。そこまで変わらないと思いますが、ちょっと無駄ですね。
実装をみてみると、最終層のxが無駄になっていますよね。Diff-SVCから受け継がれたもののようですが。

for layer in self.residual_layers:
        x, skip_connection = layer(x, cond, diffusion_step)
        skip.append(skip_connection)
x = torch.sum(torch.stack(skip), dim=0) / sqrt(len(self.residual_layers))

DDSP-SVCが弱そうなところ

　RVCと違って、HuBERT特徴量から話者情報を変換する機構がありません。そのため話者情報に依存するようなHuBERTモデルだとうまくいかなそうな気がします。ただRVCの似た特徴量を検索して線形補間をとるやつってDDSP-SVCにも適用できるので、それをすればもっと精度あがったりするのかも？？

おわりに

ここまで偉そうに語っておいて、使ったことないから実際の性能がどうなのか分からないです。ただ各設定項目の意味が割と分かってきたので、試してみる気になってきました。

2023-06-19

RVCについて

　音声変換手法の一つであるRVC(Retrieval-based-Voice-Conversion)について、色々な情報と実装を流し見して何をやっているか想像してみました。想像なのであっているかどうかはわかりません。RVCの元になっているVITSの元になっているVAEから説明していきます。
参考：
【Tensorflowによる実装付き】Variational Auto-Encoder(VAE)を理解する | 楽しみながら理解するAI・機械学習入門
 [2106.06103] Conditional Variational Autoencoder with Adversarial Learning for End-to-End Text-to-Speech
【機械学習】VITSでアニメ声へ変換できるボイスチェンジャー&読み上げ器を作った話 - Qiita
GitHub - ddPn08/rvc-webui: liujing04/Retrieval-based-Voice-Conversion-WebUI reconstruction project
最近のAIボイスチェンジャー(RVC、so-vits-svc)
RVCの構造についてのメモ
 【図解】超高性能AIボイスチェンジャー「RVC」のしくみ・コツ
 深層生成モデルを巡る旅(1): Flowベース生成モデル - Qiita
VITS学習メモ - 勾配降下党青年局

VAE(Variational Auto Encoder)

　VAEは、主に画像生成で使われるモデルです。まあ今回音声の話なので音声にしておきます。VAEは音声 $x$ の本質的な特徴をあらわす潜在変数 $z$ というものの存在を仮定する潜在変数モデルと呼ばれるものの一つです。VAEでは潜在変数の事前分布 $p(z)$ が平均0、分散1の正規分布に従うと仮定します。そして事後分布 $p(z|x)$ を予測するエンコーダ $q_\phi$ 、潜在変数 $z$ が与えられたときの音声 $x$ の分布 $p(x|z)$ を予測するデコーダ $p_\theta$ の二つを用意します。損失は音声をエンコードしてデコードしたらちゃんともとに戻るかを表す再構成誤差 $-\mathbb{E}_{q_\phi (z|x)}[\log p_\theta (x|z)]$ と、事前分布と事後分布を一致させるようにするKLダイバージェンス誤差 $D_{\mathrm{KL}}(q_\phi (z|x)\| p(z))$ を足したものになります。この損失のマイナスが実は対数尤度 $\log p(x)$ の下界となっており、またエンコーダによる事後分布の近似精度が高くなるほど対数尤度が下界に近づくため、損失の最小化⇒下界の最大化⇒対数尤度の最大化が実現できます。
　生成時は $p(z|x)$ と $p(z)$ を一致させるよう学習していることから、平均0、分散1で潜在変数をサンプリングして、それをデコードするだけで学習データっぽいデータが生成できます。ただし生成データがどんなものになるかはコントロールできません。VAEの例ではよく人間の顔をいっぱいつくっていますが、出てくる顔はおっさんとか美少女とか小五ロリとかばらばらで、あまり役に立つものではありません。

Conditional VAE(VITS)

　素のVAEでは事前分布に何も条件がなかったので、生成物をコントロールできませんでした。Condtional VAEは事前分布にテキスト条件を付けた $p(z|c)$ を用います。これにより条件 $c$ に基づいて生成することができます。ただし条件付けをする分事前分布を近似するモデルも作る必要があります。VITSでは通常のVAEのエンコーダにあたる事後分布を予測するモデルを事後エンコーダ、テキスト条件付きの事前分布を予測するモデルを事前エンコーダと呼んでいます。損失はKLダイバージェンス誤差が少し複雑になるだけですね。
　ただし音声が与えられたときの潜在変数の分布と、テキストが与えられたときの潜在変数の分布を考えるときに注意しなければならない点があります。それはテキストには発音時間の情報と話者固有の情報の二つが含まれない事です。
1. 話者固有の情報
テキストには話者固有の情報は含まれないので、このままでは事前分布には声質等が考慮されません。そこでVITSでは正規化フロー $f_\theta$ を用いた確率変数の変数変換を行います。正規化フローとはVAEと同じく潜在変数モデルの一つで、確率変数の変数変換を繰り返し、複雑な分布から簡単な分布に移動していくことで、対数尤度を直接計算することができるモデルです。そのような機能を持たせるため逆変換とヤコビアンが簡単に求められるという性質を持っています。特にVITSで使うフローはヤコビアンが1になるよう設計されています。正規化フローは潜在変数から話者固有の情報を取り除くような変数変換を行う役割をになっています。これによって事後分布と事前分布を一致しやすくしています。さらにヤコビアンが1であることからKLダイバージェンス誤差の数式にも影響しません。
2. 発音時間の情報
テキストには発音時間は含まれないので、そのままでは事後分布と事前分布を一致させることが難しくなります。学習時には各音素 $j$ 番目と各音声の時刻 $i$ 番目で $N(f_\theta(z)[i]|\mu[j],\sigma[j])$ の対数尤度を最大化するように、DP法を用いて音素と発音時刻の対応付けを行います。ここで $\mu[j],\sigma[j]$ は事前エンコーダが推測した平均や分散です。そして複数の時刻にまたがる音素について、その時刻分特徴量を複製することで、時系列を一致させます。それとともにDPで求めた発音時間を予測するモデルも学習し、推論時にはそれを使います。
　デコーダ側にも工夫があって、GANの仕組みを使うことでより自然な音声が生成できるようにしているようです。
　VITSでは各モデルに話者埋め込みを入力することによって、モデルの出力を切り替えます。これにより複数話者によるテキスト読み上げが実現できます。テキスト読み上げはテキストを事前エンコーダで潜在変数にエンコードし、正規化フローの逆変換で話者情報を付け加え、デコーダに通します。通常のVAEと同じく生成時に事後エンコーダは使われないということですね。
　おまけとして正規化フローによる話者情報の入れ替えを使うことで音声変換も可能です。音声変換は事後エンコーダで音声を潜在変数にエンコードした後、正規化フローで入力話者情報を取り除き、逆変換でターゲットの話者情報を付与します。その後デコードします。

RVC

　VITSの音声変換で不便なところは、変換先のみならず変換元の話者情報まで学習しなければいけないことです。そこでRVCではテキストではなくHuBERTの特徴量を入力にして音声生成ができるように学習します。つまり事前エンコーダへの入力を音素トークンの埋め込みベクトルからHuBERT特徴量に置き換えて、HuBERT特徴量条件付き事前分布 $p(z|h)$ を近似するよう学習します。入力が音声になるため、発音時間の情報については考慮する必要がありません。次に話者情報ですが、学習時は変換先話者の音声特徴量を入力し、推論時は変換元話者の音声特徴量を入力することになります。これでは学習時と推論時で入力の分布が変わってしまい、うまく生成できません。そこでRVCでは学習データのHuBERT特徴量を残しておき、推論時に入力した音声特徴量に近いものを検索して混ぜ合わせます。これによって推論時の入力を学習時と近づけることによってうまく生成できるようにしています。ただし近いものといってもおっさんの声を美少女の声（声のかわいさと見た目はあまり関係ないはずなのだが、どうして美少女と言ってしまうのだろうか？）を変換するときに、近いものが見つかるわけがありません。そこでピッチ変換をつかっているようです。
最終的に損失関数は、

GANの損失(Adversarial loss)
GANの認識器で中間層の出力が真贋で同じになるようにする項(Feature matching loss)
VAEの再構成誤差(Reconstruction loss)
VAEのKLダイバージェンス項(KL loss)

の4つになります。

一応実装をみておく

実装を何とか理解できる部分だけ紹介してみます。
学習時の計算っぽいところ

def forward(
    self, phone, phone_lengths, pitch, pitchf, y, y_lengths, ds
):  # 这里ds是id，[bs,1]
    # print(1,pitch.shape)#[bs,t]
    g = self.emb_g(ds).unsqueeze(-1)  # [b, 256, 1]##1是t，广播的
    m_p, logs_p, x_mask = self.enc_p(phone, pitch, phone_lengths)
    z, m_q, logs_q, y_mask = self.enc_q(y, y_lengths, g=g)
    z_p = self.flow(z, y_mask, g=g)
    z_slice, ids_slice = commons.rand_slice_segments(
        z, y_lengths, self.segment_size
    )
    # print(-1,pitchf.shape,ids_slice,self.segment_size,self.hop_length,self.segment_size//self.hop_length)
    pitchf = commons.slice_segments2(pitchf, ids_slice, self.segment_size)
    # print(-2,pitchf.shape,z_slice.shape)
    o = self.dec(z_slice, pitchf, g=g)
    return o, ids_slice, x_mask, y_mask, (z, z_p, m_p, logs_p, m_q, logs_q)

HuBERTの特徴量とピッチ情報、音声スペクトログラム、話者IDを入力としています。1行目のgは話者IDで事後エンコーダやデコーダ、フローに入力されます。enc_pが事前エンコーダ、enc_qが事後エンコーダになっていて、事前エンコーダにはHuBERT特徴量とピッチ情報が入力され、平均m_pと対数分散logs_pが出力されます。事後エンコーダには音声が入力され、潜在変数zが出力され、さらにその出力はフローを通って話者情報が取り除かれたz_pになります。デコーダにはzをランダムにスライスしたz_sliceが入力されます。これはメモリ節約のためでVITSと同じです。最終出力oはGANの認識器へ入力されるとともに、再構成誤差の計算に使われ、z_p, m_p, logs_p, logs_qはKL lossに使われます。maskはよく分かりません。

推論時の計算っぽいところ

def infer(self, phone, phone_lengths, pitch, nsff0, sid, max_len=None):
    g = self.emb_g(sid).unsqueeze(-1)
    m_p, logs_p, x_mask = self.enc_p(phone, pitch, phone_lengths)
    z_p = (m_p + torch.exp(logs_p) * torch.randn_like(m_p) * 0.66666) * x_mask
    z = self.flow(z_p, x_mask, g=g, reverse=True)
    o = self.dec((z * x_mask)[:, :, :max_len], nsff0, g=g)
    return o, x_mask, (z, z_p, m_p, logs_p)

推論はHuBERT特徴量とピッチ情報、話者IDを入力としています。話者IDに関しては学習時と同じです。事前エンコーダによって平均と分散を出力し、そこからz_pをサンプリングします。そのあと逆flowによってz_pを話者情報を含む潜在変数zに変換し、デコーダを通します。当たり前ですが学習時と違って推論時はスライスは行いません。

2023-06-12

LoRAのための特異値分解

　特異値分解を解説する記事なんていくらでもありますが、LoRAに関連付けて話す記事なんてないと思うので、ここで書いてみます。まあ自分が特異値分解を理解するためでもあります。行列の右上カッコつき添え字に行数と列数を書きます。
参考記事：
yutomiyatake.github.io

LoRA

まずLoRAについて、重み $W^{(m,n)}$ の全結合層に対して、rank= $r$ のLoRAは重みの差分 $\Delta W^{(m,n)}=A^{(m,r)}B^{(r,n)}$ を学習します。学習後の重みは $W' = W+\Delta W$ になります。LoRAは $A$ の列、 $B$ の行を分解すると、 $\Delta W^{(m,n)}=(A_1 \cdots A_r) \begin{pmatrix} B_1 \\ \vdots \\ B_r\end{pmatrix}=\displaystyle{\sum_{i=1}^{r}A_i^{(m,1)}B_i^{(1,n)}}$
となって、rank= $1$ のLoRAをrank個分合計したような形になっています。

特異値分解

特異値分解は $\mathrm{rank}(W)=r$ の行列 $W^{(m,n)}$ を、

$W^{(m,n)}=U^{(m,m)}\Sigma^{(m,n)}V^{(n,n)}= U^{(m,m)} \begin{pmatrix} \sigma_{1} & & & & & \\ & \ddots & & & \huge{0} & \\ & & \sigma_{r} & & & \\ & & & 0 & & \\ & \huge{0} & & & \ddots & \\ & & & & & 0 \end{pmatrix} V^{(n,n)}$

とする操作です。ここで $U,V$ は直交行列（転置すると逆行列になる行列）で、 $\sigma_1,\cdots ,\sigma_r$ は特異値と呼ばれるものです。
図にすると以下のような形に変形できます。

どんどんLoRAと似たような形になっていくことが分かるでしょうか。

特異値分解の方法

$U,V$ が直交行列であることを考えると、
$\begin{eqnarray} W^TW &=&(U\Sigma V)^TU\Sigma V \\ &=&V^T\Sigma^TU^TU\Sigma V \\ &=&V^T \Sigma^T \Sigma V \\ &=&V^T\begin{pmatrix} \sigma_{1}^2 & & & & & \\ & \ddots & & & \huge{0} & \\ & & \sigma_{r}^2 & & & \\ & & & 0 & & \\ & \huge{0} & & & \ddots & \\ & & & & & 0 \end{pmatrix} V \end{eqnarray}$

$\begin{eqnarray} WW^T &=&U\Sigma V (U\Sigma V)^T \\ &=&U\Sigma V V^T\Sigma^T U^T \\ &=&U \Sigma \Sigma^T U^T \\ &=&U \begin{pmatrix} \sigma_{1}^2 & & & & & \\ & \ddots & & & \huge{0} & \\ & & \sigma_{r}^2 & & & \\ & & & 0 & & \\ & \huge{0} & & & \ddots & \\ & & & & & 0 \end{pmatrix} U^T \end{eqnarray}$

となります。これは対角化の形になっていますね。つまり $WW^T,W^TW$ の固有ベクトルを計算すれば、 $U,V$ を求めることができます。特異値は固有値の平方根になっています。実装上でどうやってるかは知らないですけど、アルゴリズム的には解けることはわかりますね。

特異値分解とrank

正則行列をかけても階数が変わらないという性質を考えると、 $\mathrm{rank}(A)=\mathrm{rank}(U\Sigma V)=\mathrm{rank}(\Sigma)$ になります。 $\Sigma$ は対角成分以外が0の行列ですので、非零の対角成分の個数がrankと一致します。つまり特異値の数がrankと一致します。

低ランク近似

特異値分解した結果、 $A=U\Sigma V=\displaystyle{\sum_{i=1}^{r}}\sigma_iU_iV_i$ で、特異値 $\sigma_1,\dots,\sigma_r$ は大きい順にソートされているとします。すると上位 $k$ 個の特異値のみを使った行列で近似することができます。 $A\fallingdotseq \tilde{A_k}=U\Sigma_{[\sigma_{k+1},\dots,\sigma_r:=0]}V=\displaystyle{\sum_{i=1}^{k}}\sigma_iU_iV_i$ です。0でない対角成分が $k$ 個となるわけですから、 $\mathrm{rank}(A_k)=k$ となります。この近似を低ランク近似と呼びます。

特異値分解によるLoRAの抽出

特異値分解によって、LoRAの抽出が行えます。事前学習済みモデルの重み $W$ に対して、何らかのファインチューニングモデル $W'$ があるとすると、学習差分 $\Delta W = W'-W$ をLoRAの形 $AB$ に変換することができます。 $\Delta W$ を特異値分解すれば、 $\Delta W = \displaystyle{\sum_{i=1}^{r}}\sigma_iU_iV_i$ の形に変換できます。すると低ランク近似により、ランク $k$ のLoRAに近似できます。具体的には $\tilde{\Delta W_k}=\displaystyle{\sum_{i=1}^{k}}\sigma_iU_iV_i$ で、 $A=(\sigma_1U_1 \cdots \sigma_{k} U_{k})$ , $B=V_{1:k}$ のようにすればできます。 $\sigma$ は $A$ と $B$ どっちに入れてもいいですけどね。

LoRAのリサイズ

任意のLoRAをそれより小さいランクのLoRAに近似することもできます。といってもほぼ抽出と同じで、LoRAの $AB=\Delta W$ を計算して後は低ランク近似を用いて同様の操作をするだけです。ところでKohya氏によるLoRAのリサイズには $k$ を自動で決める実装があります。決め方に三通りあります。何らかの閾値 $r$ を決めて、

最大特異値に対して $r$ %の大きさまでの特異値を選ぶ。
特異値の累積和を求めて全体の $r$ %以上になるまで特異値を選ぶ。
特異値の累積二乗和を求めて全体の $r^2$ %以上になるまで特異値を選ぶ。

直感的には上の二つが分かりやすそうですが、3つ目には数学的な意味があります。

LoRAのマージ

LoRAのマージには重みをそのままマージする方法と、特異値分解を行う方法があります。
二つのLoRAをマージするとき、やりたいことは $\Delta W_1 + \Delta W_2 = A_1B_1 + A_2B_2$ となります(weightは省略)。しかし単に全重みをマージしたLoRAは、 $(A_1+A_2)(B_1+B_2)=A_1B_1+A_1B_2+A_2B_1+A_2+B_2$ となって目標とは違うものになってしまいます。特異値分解を行う方法では、 $A_1B_1 + A_2B_2$ の低ランク近似を行います。これも近似ではありますが、全く別のLoRAをマージするときは特異値分解を行う方法の方が精度が高くなりそうです。ちなみにランクが上がってしまいますが、 $A=(A_1 A_2), B = \begin{pmatrix} B_1 \\ B_2 \end{pmatrix}$ とすればマージ・・というかただの結合ですが精度を落とさず一つのLoRAにできます。

特異値とフロベニウスノルム

フロベニウスノルムとは、行列の各要素の二乗和の平方根です。 $\|A\|_F=\sqrt{\displaystyle{\sum_{i}\sum_{j}}a_{ij}^2}$ という感じです。ユークリッド距離をそのまま行列に適用したような形ですね。実は特異値の二乗和はフロベニウスノルムの二乗と一致します。まずそれを確認します。
補題1. $\|A\|_F^2=\mathrm{tr}(AA^T)=\mathrm{tr}(A^TA)$ ( $\mathrm{tr}$ は対角成分の和です。)
証明：
$A$ を $(m,n)$ 行列とすると、 $(AA^T)_{ij}=\displaystyle{\sum_{k=1}^{n}}a_{ik}a_{jk}$ ですので、対角成分は、 $(AA^T)_{ii}=\displaystyle{\sum_{k=1}^{n}}a_{ik}a_{ik}$ となり
$\mathrm{tr}(AA^T)= \displaystyle{\sum_{i=1}^m}(AA^T)_{ii}=\displaystyle{\sum_{i=1}^m}\displaystyle{\sum_{k=1}^{n}}a_{ik}a_{ik}=\|A\|_F^2$ です。 $A^TA$ の場合も多分同じようなもん。
補題2. 直交行列をかけてもフロベニウスノルムは変わらない。つまり $\|A\|_F=\|UA\|_F=\|AV\|_F$
証明：
$\|UA\|_F^2=\mathrm{tr}((UA)^TUA)=\mathrm{tr}(A^TU^TUA)=\mathrm{tr}(A^TA)=\|A\|_F^2$
$\|AV\|_F^2=\mathrm{tr}(AV(AV)^T)=\mathrm{tr}(AVV^TA^T)=\mathrm{tr}(AA^T)=\|A\|_F^2$
補題1を使ってます。正の数なので両辺のルートをとれば成立です。系として両側からかけても $\|UAV\|_F=\|UA\|_F=\|A\|_F$ となります。

定理：特異値の二乗和＝フロベニウスノルムの二乗
特異値分解された形を考えれば、補題2を使って、
$\|A\|_F^2=\|U\Sigma V\|_F^2 = \|\Sigma\|_F^2 = \displaystyle{\sum_{i=0}^{r}\sigma_i^2}$

つまりLoRAのリサイズに特異値の二乗和を利用するのは、フロベニウスノルムを使った行列間の距離に基づく方法になります。閾値を $r^2$ %としたのは特異値の累積二乗和の平方根をとるより閾値を二乗したほうが計算も実装が楽だからだと思います。

低ランク近似の根拠

LoRAの抽出において、特異値を大きい順にソートして、 $k$ 個で打ち切ることで近似しましたが、これには根拠があります。以下の定理が成り立ちます。
エッカート・ヤングの定理.
$\displaystyle{\mathrm{argmin}_{X,\mathrm{rank}(X)\leq k}} \| A-X\|_F = \tilde{A_k}$
ここで $\tilde{A_k}$ は低ランク近似を行った行列です。つまり低ランク近似はフロベニウスノルムを距離としたときに最適な近似ということです、
証明：
$A=U\Sigma V$ と特異値分解できるとすると、
$\begin{eqnarray} \| A-X\|_F^2 &=& \| U^T(A-X)V^T\|_F^2 \\ & = & \mathrm{tr}(U^T(A-X)V^T(U^T(A-X)V^T)^T) \\ & = & \mathrm{tr}((U^TAV^T-U^TXV^T)(U^TAV^T-U^TXV^T)^T ) \\ & = & \mathrm{tr}((\Sigma-U^TXV^T)(\Sigma-U^TXV^T)^T ) \\ & = & \|\Sigma - U^TXV^T \|_F^2 \end{eqnarray}$
となります。ここで $U^TXV^T=G$ として、 $(i,j)$ 要素を $g_{ij}$ とすると、
$\begin{eqnarray} \| A-X\|_F^2 &=& \|\Sigma - U^TXV^T \|_F^2 \\ & = & \displaystyle{\sum_{i=1}^{r}(\sigma_i - g_{ii})^2} + \displaystyle{\sum_{i=k+1}^{m}g_{ii}^2} + \displaystyle{\sum_{i\neq j}g_{ij}^2} \end{eqnarray}$

ここで $\mathrm{rank}(X)=\mathrm{rank}(G)$ となるので、上の値と $G$ のrankをなるべく小さくしたいですね。このとき $i=k+1,\dots,r$ までの $g_{ii}$ と $i\neq j$ で $g_{ij}$ は0にすればrankも $\| A-X\|_F$ もあがりません。あとは $i=1,\dots,k$ での、 $g_{ii}$ です。これはそれぞれ、 $g_{ii}=\sigma_i$ とすれば0になりますが、rankの制限のことを考えると、0より大きくしていいのは最大 $k$ 個です。そこで大きい順から $k$ 個選んで、それ以外を0とすれば最適解になります。これはまさに $\Sigma_{[\sigma_{k+1},\dots,\sigma_r:=0]}$ そのものであり、 $X=UGV=A_k$ になります。

LoConの特異値分解

いままでは全結合層の重みについて話していきましたが、畳み込みニューラルネットワークでも同様の操作が行えます。LoConですね。畳み込みニューラルネットワークは、フィルター1回分の計算を考えてみると、入力チャンネル×フィルターサイズ→出力チャンネル×1の全結合層になります。この全結合層を位置を動かしながら適用するだけです。

フィルターサイズ3×3の畳み込み層の重みを $W^{(m\times 9,n)}$ とすれば、LoConは $\Delta W^{(m\times 9,n)} = A^{(m\times 9,r)}B^{(r,n)}$ であり、要素の順番さえ気をつかえば特異値分解によるLoRA抽出も行えます。
CP分解についてはLyCORISで実装されていますが特異値分解とはまた別の分解でありよく分かっていません。
upの方を3×3にする方式は多分特異値分解による抽出は出来ないと思います。down層はin×9次元からrank×9次元への変換ですが、実際には9マスそれぞれ同じ重みを共有しているからです。つまり $\Delta W = A^{(m\times 9,r \times 9)}B^{(r \times 9,n)}$ としたいのですが、実際にはdownは $A^{(m\times 9,r \times 9)}$ ではなく、 $A^{(m,r)}$ になります。ただし特異値分解による抽出ができないだけで、マージはできます。2×2を2回適用する方法も特異値分解できないと思います。こっちはもはや行列としても表現しにくいです。ただしこちらもマージはできます。まあこの辺多分そうでしょうという感じで語ってます。

まとめ

LoRAは特異値分解のような形状になっている。そのため特異値分解によってリサイズや抽出ができる。
特異値分解による低ランク近似はフロベニウスノルムに基づいており、特異値の二乗和によって計算できる。
畳み込みのLoRAで特異値分解の形をしているのは、downを3×3の畳み込み、upを1×1にする方法のみっぽい。

2023-06-02

noise_predictionモデルとv_predictionモデルの損失

　Stable-Diffusionのv1系は画像に加わったノイズを予測するモデルですが、v2の一部はvelocityというものを予測しています。この2つは損失関数が違うのでlossで比べられません。経験的にv_predictionモデルの方が3倍くらいlossが大きくなるイメージですが、数学的に確認していきます。
　

ノイズが加わった画像について

元の画像を $x_0$ 、ノイズを $\epsilon$ とすると時刻 $t\in [1,\cdots,1000]$ でノイズが加えられた画像は $x_t=\sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}}\epsilon$ という式で表されます。 $x_0$ はVAEエンコーダの出力である潜在変数なので、平均0で分散1の正規分布に従っています。ノイズはそもそも実装として平均0で分散1の正規分布です。めんどくさいので $a_t=\bar{\alpha_t},\ \sigma_t=\sqrt{1-\bar{\alpha_t}}$ とします。すると画像の分散は $a_t^2$ 、ノイズの分散は $\sigma_t^2$ になります。

velocity[1]について

　 $a_t^2+\sigma_t^2=1$ であることに注目すると、時刻 $t$ ごとにある角度 $\phi_t$ があって、 $a_t=\cos \phi_t,\ \sigma_t=\sin \phi_t$ で表されます。そうすると $x_t=\cos \phi_t x_0 + \sin \phi_t \epsilon$ となります。これを角度で微分したものがvelocityです。 $v=\frac{dx_t}{d\phi_t}= - \sin \phi_t x_0 + \cos \phi_t \epsilon= a_t \epsilon - \sigma_t x_0$ となります。図にすると以下のようになります。

ノイズを加えていく拡散過程を円運動ととらえて、velocityはその速度になるわけですね。

信号対雑音比

　ここで信号対雑音比(s/n比、SNR)というものを紹介します。これは $\mathrm{SNR}=\frac{\text{信号の分散}}{\text{雑音の分散}}=\frac{a_t^2}{\sigma_t^2}$ で求まり、ノイズが小さい画像は大きくなり、ノイズが大きい画像ほど小さくなります。この信号対雑音比を考えると、ノイズ $\epsilon$ を予測するモデルとvelocity $v$ を予測するモデルと元の画像 $x_0$ を予測するモデルが統一的に考えられます。モデルが予測した値に $\hat{}$ をつけるとそれぞれのモデルの損失の関係は以下のようになります。[2]で紹介されています。
$\begin{eqnarray} \|\epsilon - \hat{\epsilon}\|^2 &=& \|\frac{x_t-a_t x_0 }{\sigma_t} - \frac{x_t-a_t\hat{x_0}}{\sigma_t}\|^2 \\ &=& \|-\frac{a_t}{\sigma_t}(x_0 - \hat{x_0})\|^2 \\ &=& \frac{a_t^2}{\sigma_t^2}\|x_0 - \hat{x_0}\|^2 \\ &=& \mathrm{SNR}(t)\|x_0 - \hat{x_0}\|^2 \end{eqnarray}$

入力におけるノイズが占める割合が少ないとき(SNRが大きいとき)は $x_0$ の予測は簡単で、 $\epsilon$ の予測が難しくなります。この事実が損失関数の関係に現れていますね。極端な話をするとSNRが0のとき、つまり入力がノイズのときノイズ予測モデルでは損失が0になります。入力をそのまま出力するだけなんだから当然ですね。

$\begin{eqnarray} \|v - \hat{v}\|^2 &=& \|a_t \epsilon-\sigma_t x_0 - (a_t \hat{\epsilon} - \sigma_t\hat{x_0})\|^2 \\ &=& \|a_t(\epsilon - \hat{\epsilon}) -\sigma_t(x_0 - \hat{x_0})\|^2 \\ &=& \|a_t(\frac{x_t-a_t x_0 }{\sigma_t} - \frac{x_t-a_t\hat{x_0}}{\sigma_t}) -\sigma_t(x_0 - \hat{x_0})\|^2 \\ &=& \|-\frac{a_t^2}{\sigma_t}(x_0-\hat{x_0}) -\sigma_t(x_0 - \hat{x_0})\|^2 \\ &=& |-\frac{a_t^2+\sigma_t^2}{\sigma_t}(x_0 - \hat{x_0})\|^2 \\ &=& |-\frac{1}{\sigma_t}(x_0 - \hat{x_0})\|^2 \\ &=& (\frac{1}{\sigma_t^2})\|(x_0 - \hat{x_0})\|^2 \\ &=& (\frac{a_t^2+\sigma_t^2}{\sigma_t^2})\|(x_0 - \hat{x_0})\|^2 \\ &=& (\mathrm{SNR}(t)+1)\|x_0 - \hat{x_0}\|^2 \\ &=& \frac{\mathrm{SNR}(t)+1}{\mathrm{SNR}(t)}\|\epsilon - \hat{\epsilon}\|^2 \end{eqnarray}$

つまりv_predictionモデルは $\frac{\mathrm{SNR}(t)+1}{\mathrm{SNR}(t)}$ だけ損失が大きくなるということですね。これがどのくらいの値なのか調べてみましょう。

import torch
from diffusers import DDPMScheduler
import matplotlib.pyplot as plt
scheduler = DDPMScheduler.from_pretrained("stabilityai/stable-diffusion-2", subfolder="scheduler")

timesteps = torch.arange(0,1000)

def get_snr(
    scheduler, 
    timesteps: torch.IntTensor,
) -> torch.FloatTensor:

    sqrt_alpha_prod = scheduler.alphas_cumprod[timesteps] ** 0.5
    sqrt_alpha_prod = sqrt_alpha_prod.flatten()

    sqrt_one_minus_alpha_prod = (1 - scheduler.alphas_cumprod[timesteps]) ** 0.5
    sqrt_one_minus_alpha_prod = sqrt_one_minus_alpha_prod.flatten()

    return (sqrt_alpha_prod / sqrt_one_minus_alpha_prod) ** 2

snr = get_snr(scheduler, timesteps)

plt.xlabel("timesteps")
plt.ylabel("(snr+1)/snr")
plt.plot(timesteps,(snr+1)/snr)

こうしてみると $t$ が大きいとき、つまりノイズが大きいときに損失が大きくなりやすいですね。グラフ見ただけではわかりませんが、時刻が0に近いとき値は1に近づいています（式を考えれば当然ですけど）。velocityを予測するモデルでは、 $\epsilon$ と $x_0$ の両方を予測する必要があるため、ノイズ予測モデルのようにノイズが大きいときは予測が簡単という関係になりにくいです。よって各時刻における予測難易度のバランスがとれているということですね。このグラフの平均をとればv_predictionでどのくらいlossが大きくなるはずか計算できるのかなと思ったんですが、そうじゃないみたいですね。単純に平均すればいいってわけじゃないみたいですね。

v_predictionモデルでnoise_predictionのように学習する？

v2系はv1系に比べて評価が低いです。理由として考えられるのは以下の三点です。

テキストエンコーダが悪い
あんな画像を学習しないのが悪い
v_predictionモデルが悪い

1.に関してはよく知りませんが、v1系と違うものなので可能性はあります。

2.に関してはv2系はあんな画像を結構弾いたらしいので、基盤モデルとしてアニメ調の画像の性能が悪いのかもしれません。

そして3.が今回の話です。ノイズ予測モデルと比べて、ノイズが大きいときの損失が大きくなるので、大まかな要素の学習を優先して、細部の学習を怠ってしまうのかもしれません。これが原因ならば幸いファインチューニングで修正できる可能性はあります。損失に $\frac{\mathrm{SNR}(t)}{\mathrm{SNR}(t)+1}$ をかけるだけでノイズ予測モデルと同様の学習ができます。

参考記事

[1][2202.00512] Progressive Distillation for Fast Sampling of Diffusion Models
[2][2303.09556] Efficient Diffusion Training via Min-SNR Weighting Strategy

2023-05-29

ネガティブプロンプトの理論とPerp-Neg

　ネガティブプロンプトに関する面白そうな論文を見つけたので、ちょっと読んでみますが、その前にネガティブプロンプトの理論的な背景について自分なりの解釈でまとめてみます。
arxiv.org
いきなりですが、拡散モデルはスコアベースモデルと解釈できて、ノイズを予測するモデルは推定値がスコアと比例します。
$\nabla_x \log p(x) = -\frac{1}{\sigma_t}\hat{\epsilon}(x,t)$
このスコアというのは、今回は理解する必要はないです（私もそんな理解してないし）。確率分布で一番難しい分配関数（足して1になるための積分）が計算に必要ないので導出しやすいという性質を持ち、拡散モデルの背景の一つになっています。

分類器誘導(Classifier guidance)

拡散モデルの生成に条件を付けるため、分類器誘導と呼ばれる手法では、以下のような計算により与える条件に近づくようにスコアを誘導します。
$\nabla_x \log p_{\gamma}(x|c) = \gamma\nabla_x \log p(c|x) + \nabla_x \log p(x)$
第一項のスコアは何らかの分類器を用いて計算します。たとえばおっぱいが小さい子を生成したい場合は、おっぱい分類器を用いて、 $c=$ "おっぱいが小さい"に近づくような $x$ の方向を求めてそっちに誘導します。ここで条件をどれだけ重視するかを $\gamma$ という値で決めていて、大きくすれば条件に忠実になるが生成画像の多様性が低くなります。
この分類器誘導という手法は拡散モデルの他に別の分類器を作らなければいけないこと、さらにノイズに頑強なモデルである必要があることから、使いにくいです。そこで拡散モデルそのものに分類器としての機能を持たせるのが分類器無し誘導です。

分類器無し誘導(Classifier free guidance)

$\begin{eqnarray} \nabla_x \log p_{\gamma}(x|c) &=& \gamma\nabla_x \log p(c|x) + \nabla_x \log p(x) \\ &=& \gamma\nabla_x \log \frac{p(x|c)p(c)}{p(x)} + \nabla_x \log p(x) (\text{ベイズの定理})\\ &=& \gamma(\nabla_x \log p(x|c) - \nabla_x \log p(x)) + \nabla_x \log p(x) \\ &&(x\text{の微分なので}p(c)\text{に関する項は消える}) \end{eqnarray}$

これがCFGの式です。 $\gamma$ がCFG scaleとかguidance scaleと呼ばれるものです。これを使うためには、条件付きの推定と、無条件の推定の両方を学習する必要があります。txt2imgモデルでは、学習中に10%くらいの確率でテキストを空文にするだけでいいらしいです。

ネガティブプロンプトのCFG

では複数条件になるとどうなるでしょうか？とりあえず二条件にしてみます。

$\begin{eqnarray} \nabla_x \log p_{\gamma}(x|c_1,c_2) &=& \gamma\nabla_x \log p(c_1,c_2|x) + \nabla_x \log p(x) \\ &=& \gamma\nabla_x \log p(c_1|x)p(c_2|x) + \nabla_x \log p(x) (\text{二つの条件が独立なら・・・})\\ &=& \gamma\nabla_x \log \frac{p(x|c_1)p(c_1)}{p(x)}\frac{p(x|c_2)p(c_2)}{p(x)} + \nabla_x \log p(x) (\text{ベイズの定理})\\ &=& \gamma(\nabla_x \log p(x|c_1) - \nabla_x \log p(x)) \\ && +\gamma(\nabla_x \log p(x|c_2) - \nabla_x \log p(x)) \\ && + \nabla_x \log p(x) \end{eqnarray}$

3つ4つと増やしても項がどんどん増えるだけで式の形は同じです。webuiのAND構文を使えばこれを使った生成ができます。 $\gamma$ について、二条件で別々のものを使うことも考えられます（この辺の理論的裏付けは分からない）。たとえば1つ目の条件を目標の条件 $c_{\mathrm{pos}}$ 、2つ目の条件の係数に $\gamma$ ではなく $-\gamma$ を使えば、望ましくない要素( $c_{\mathrm{neg}}$ )を排除するような式が出てきます。
$\gamma(\nabla_x \log p(x|c_{\mathrm{pos}}) - \nabla_x \log p(x)) - \gamma(\nabla_x \log p(x|c_{\mathrm{neg}}) - \nabla_x \log p(x)) + \nabla_x \log p(x) \\ =\gamma(\nabla_x \log p(x|c_{\mathrm{pos}}) - \nabla_x \log p(x|c_{\mathrm{neg}})) + \nabla_x \log p(x)$

これがほとんどネガティブプロンプトになるわけですが、このままだと二つの条件と無条件の3つのノイズ推定を行う必要があります。そこで上の式を以下に置き換えます。
$\gamma(\nabla_x \log p(x|c_{\mathrm{pos}}) - \nabla_x \log p(x|c_{\mathrm{neg}})) + \nabla_x \log p(x|c_{\mathrm{neg}})$

これがAUTOMATIC1111氏が実装したネガティブプロンプトです。これなら二つのノイズ予測で済みます。 $\gamma$ が十分大きければほとんど同じ値になるからおっけーってことなんでしょうね。実装的にも上の単一条件での式の無条件部分にネガティブプロンプトを入れるだけなので、めちゃくちゃ楽です。

予測対象ごとの式

ノイズ予測モデルの場合

ノイズの予測がスコアと比例することから、すぐに以下の式がでてきます。
$\hat {\epsilon} = \hat {\epsilon} (x|c_{\mathrm{neg}}) + \gamma (\hat {\epsilon} (x|c_{\mathrm{pos}}) - \hat {\epsilon} (x|c_{\mathrm{neg}}))$

ノイズのない画像を予測するモデルの場合

$\begin{eqnarray} \hat {x} &=& \frac{1}{\alpha_t}(x - \sigma_t \hat{\epsilon}) \\ &=& \frac{1}{\alpha_t}(x - \sigma_t (\hat {\epsilon} (x|c_{\mathrm{neg}}) + \gamma (\hat {\epsilon} (x|c_{\mathrm{pos}}) - \hat {\epsilon} (x|c_{\mathrm{neg}}))))\\ &=& \frac{1}{\alpha_t}(x - \sigma_t \hat {\epsilon} (x|c_{\mathrm{neg}})) + \gamma(\frac{1}{\alpha_t}(x - \sigma_t\hat {\epsilon} (x|c_{\mathrm{pos}})) - \frac{1}{\alpha_t}(x- \sigma_t\hat {\epsilon} (x|c_{\mathrm{neg}}))) \\ &=& \hat {x} (x|c_{\mathrm{neg}}) + \gamma (\hat {x} (x|c_{\mathrm{pos}}) - \hat {x} (x|c_{\mathrm{neg}})) \end{eqnarray}$

velocityを予測するモデルの場合、

$\begin{eqnarray} \hat{v}&=&\sigma_t \hat{x} - \alpha_t \hat{\epsilon} \\ &=& \sigma_t(\hat {x} (x|c_{\mathrm{neg}}) + \gamma (\hat {x} (x|c_{\mathrm{pos}}) - \hat {x} (x|c_{\mathrm{neg}}))) - \alpha_t(\hat {\epsilon} (x|c_{\mathrm{neg}}) + \gamma (\hat {\epsilon} (x|c_{\mathrm{pos}}) - \hat {\epsilon} (x|c_{\mathrm{neg}}))) \\ &=& \sigma_t \hat{x} (x|c_{\mathrm{neg}}) - \alpha_t\hat {\epsilon} (x|c_{\mathrm{neg}}) + \gamma(\sigma_t \hat{x}(x|c_{\mathrm{pos}}) - \alpha_t\hat {\epsilon} (x|c_{\mathrm{pos}})-(\sigma_t \hat{x}(x|c_{\mathrm{neg}}) - \alpha_t\hat {\epsilon} (x|c_{\mathrm{neg}}))) \\ &=& \hat {v} (x|c_{\mathrm{neg}}) + \gamma (\hat {v} (x|c_{\mathrm{pos}}) - \hat {v} (x|c_{\mathrm{neg}})) \end{eqnarray}$

となり $\epsilon,x,v$ を除いて同じ式になります。つまり予測対象に関わらずUNetの出力にそのままこの式を適用すればいいだけになります。

Perp-Neg

いよいよ論文の中身に入っていきますがそんなに分かってません。特にこの論文は3D生成のための話らしいですが、あんまり興味ないのでその辺は読んでません。複数条件の式を出すとき、さらっと二つが独立であればとか言いましたが、実際独立なわけありません。このままだとポジティブプロンプトとネガティブプロンプトの間で重なるような情報を打ち消しあってしまいます。そこでPerp-negではポジティブプロンプトに対して垂直なスコアを利用します。図としてまとめてみたら割と何やってるかは分かったので、貼り付けます。

適当に書くと最終的な式は以下のようになります。
$\hat {\epsilon} = \hat {\epsilon} (x|c_{\mathrm{neg}}) + \gamma (\hat {\epsilon} (x|c_{\mathrm{pos}}) - \hat {\epsilon} (x|c_{\mathrm{neg}})^{\perp})$
ただし論文には複数のネガティブプロンプトをそれぞれ重み付けしたものを使っています。
ネガティブプロンプトの改良ということで話は面白いんですが、AUTOMATIC1111氏のネガティブプロンプトは、ポジティブとネガティブの二つのノイズ予測のみで計算できるという大きな利点があります。3D生成のような複雑なタスクではなく単純な画像生成なら、多少理論的な厳密性を無視して効率のよい計算式で何枚も生成する方がよさそうなのがつまらないですね。
WebUIの拡張スクリプトを作ってみました。できたばっかりなのでちゃんとできてるか分かりませんけど。
GitHub - laksjdjf/Perp-Neg-stablediffusion-webui

2023-04-25

クロネッカー積のランク

LyCORISのlokrで使われる、クロネッカー積とランクの関係が気になったので、検索してみたのですが、
日本語の記事は全く見つからずよく分からない英語の情報だけ見つかったので、その証明を確認してみます。
math.stackexchange.com

クロネッカー積とは行列 $A,B$ に対して、以下のような行列を返す演算です。
$A \otimes B = \begin{pmatrix} a_{11}B & \cdots & a_{1n}B \\ \vdots & \ddots & \vdots \\ a_{m1}B &\cdots & a_{mn}B \\ \end{pmatrix}$

$(m,n)$ 行列と $(p,q)$ 行列に対してクロネッカー積を適用すると、 $(mp,nq)$ 行列になります。

$\mathrm{rank}(A\otimes B) = \mathrm{rank}(A)\mathrm{rank}(B)$ になるらしく、その証明を目指します。

補題1.

行列 $A,B,C,D$ に対して、 $AC$ や $BD$ が定義できるサイズのとき、
$(A\otimes B)(C\otimes D) = AC\otimes BD$
証明.
$\begin{eqnarray} (A\otimes B)(C\otimes D) & =& \begin{pmatrix} a_{11}B & \cdots & a_{1n}B \\ \vdots & \ddots & \vdots \\ a_{m1}B &\cdots & a_{mn}B \\ \end{pmatrix} \begin{pmatrix} c_{11}D & \cdots & c_{1l}D \\ \vdots & \ddots & \vdots \\ c_{n1}D &\cdots & c_{nl}D \\ \end{pmatrix} \\ &=&\begin{pmatrix} {\displaystyle\sum_{k=1}^{n}} a_{1k}c_{k1}BD & \cdots & {\displaystyle\sum_{k=1}^{n}} a_{1k}c_{kl}BD \\ \vdots & \ddots & \vdots \\ {\displaystyle\sum_{k=1}^{n}} a_{mk}c_{k1}BD &\cdots & {\displaystyle\sum_{k=1}^{n}} a_{mk}c_{kl}BD \\ \end{pmatrix} \\ &=&\begin{pmatrix} {\displaystyle\sum_{k=1}^{n}} a_{1k}c_{k1} & \cdots & {\displaystyle\sum_{k=1}^{n}} a_{1k}c_{kl} \\ \vdots & \ddots & \vdots \\ {\displaystyle\sum_{k=1}^{n}} a_{mk}c_{k1} &\cdots & {\displaystyle\sum_{k=1}^{n}} a_{mk}c_{kl} \\ \end{pmatrix} \otimes BD \\ &=& AC\otimes BD \end{eqnarray}$

補題2.

$A,B$ が正則行列のとき、 $A\otimes B$ も正則行列。
逆行列は $(A\otimes B)^{-1}= A^{-1}\otimes B^{-1}$
証明.
$A$ を $(m,m)$ 行列、 $B$ を $(n,n)$ 行列とすると、補題1を使って、
$\begin{eqnarray} (A\otimes B)(A^{-1}\otimes B^{-1}) &=& AA^{-1} \otimes BB^{-1} \\ & =& I_m \otimes I_n \\ &=&\begin{pmatrix} I_n & & \huge{0} \\ & \ddots & \\ \huge{0} && I_n \\ \end{pmatrix} (m行) \\ &=& I_{mn} \end{eqnarray}$

補題3.

正則行列をかけてもrankは変わらない。つまり正則行列 $B,C$ と任意の行列 $A$ に対して、
$\mathrm{rank}(AB) = \mathrm{rank}(A)$
$\mathrm{rank}(CA) = \mathrm{rank}(A)$

証明.
以下のリンクに丸投げ。
行列のランクの定義・例・性質/公式 (証明付) - 理数アラカルト -

定理.

任意の行列 $A,B$ に対して、
$\mathrm{rank}(A\otimes B) = \mathrm{rank}(A)\mathrm{rank}(B)$
証明.
$\mathrm{rank}(A) = r, \mathrm{rank}(B) = s$ とする。
行列 $A,B$ を特異値分解すると、
$A = U_A\Sigma_A V_A, B=U_B\Sigma_B V_B$
ここで、 $\Sigma_A$ は下みたいな感じの行列です。
$\Sigma_A = \begin{pmatrix} \sigma_{1} & & & & & \\ & \ddots & & & \huge{0} & \\ & & \sigma_{r} & & & \\ & & & 0 & & \\ & \huge{0} & & & \ddots & \\ & & & & & 0 \end{pmatrix}$
なんかずれてる・・・？たすけて。 $\sigma_1 , \cdots, \sigma_r$ は0でない $A$ の特異値です。また $U_A,V_A,U_B,V_B$ は直交行列（つまり正則行列でもある）です。

補題2より、 $U_A^{-1}\otimes U_B^{-1},\ V_A^{-1}\otimes V_B^{-1}$ は正則行列であり、補題3より
$\mathrm{rank}(A\otimes B) = \mathrm{rank} ( (U_A^{-1}\otimes U_B^{-1})(A\otimes B)(V_A^{-1}\otimes V_B^{-1}) )$

ここで、補題1を使って、
$\begin{eqnarray} (U_A^{-1}\otimes U_B^{-1})(A\otimes B)(V_A^{-1}\otimes V_B^{-1}) &=& (U_A^{-1}A V_A^{-1}) \otimes (U_B^{-1} B V_B^{-1}) \\ &=& \Sigma_A \otimes \Sigma_B \\ &=& \begin{pmatrix} \sigma_{1}\Sigma_B & & & & & \\ & \ddots & & & \huge{0} & \\ & & \sigma_{r}\Sigma_B & & & \\ & & & 0 & & & \\ & \huge{0} & & & \ddots & \\ & & & & & 0 \end{pmatrix} \\ \end{eqnarray}$
この行列は、非零の対角成分が $rs$ 個でそれ以外の成分がすべて0の行列です。つまりランクは $rs$ です。
よって、
$\begin{eqnarray} \mathrm{rank}(A\otimes B) &=& \mathrm{rank} ( (U_A^{-1}\otimes U_B^{-1})(A\otimes B)(V_A^{-1}\otimes V_B^{-1}) ) \\ & = & rs \\ & = & \mathrm{rank}(A)\mathrm{rank}(B) \end{eqnarray}$

証明終わり。

おわりに

記事の確認中、ためしに編集画面の文字列そのままGPT4に貼り付けたら、インデックスの間違いを指摘してくれました・・・（補題1中の $\sum$ の上付き添え字を $m$ にしてた）。もうAIには勝てません。